엔탈피 ( Enthalpy )
: 일정한 압력과 온도에서 어떤 물질이 가지고 있는 고유한 에너지의 함량
엔탈피와 차후 배우게 될 엔트로피의 개념은 열역학에서 매우 중요한 개념입니다. 엔탈피는 엔트로피와 더불어 물질계의 안정성과 변화의 방향, 그리고 화학 평형의 위치와 이동을 결정하는 핵심적인 요소이며 반응 전후의 온도를 같게 하기 위하여 계가 흡수하거나 방출하는 열(에너지)을 의미합니다.
엔탈피는 다음과 같이 표현됩니다. ( 엔탈피와 열역학 제1법칙과의 관계는 다음 글에서 이어나가겠습니다. )
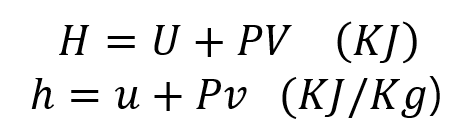
그러나 물질이 가진 에너지의 절대량은 알 수 없습니다. 반응이 일어날 때의 반응 물질의 엔탈피와 생성 물질의 엔탈피의 차이만 알 수 있으므로 반응이 일어날 때에는 이 차이에 해당하는 에너지가 감소하거나 증가하는데, 엔탈피가 감소할 때에는 에너지가 열로 방출되며, 엔탈피가 증가할 때에는 증가한 만큼의 에너지가 외부에서 흡수되기 때문입니다.

엔탈피를 구하기 위해서는 내부 에너지와 압력, 그리고 체적에 대해서 파악해야 합니다. 해당 요소들은 모두 Property Table에 나타나 있는데 비체적 같은 경우에는 순수 물질의 상태에 따라서 다양한 값을 가지고 있습니다. 다양한 상태라고 하면 전 포스트에서 적었던 Property Diagram에서 나타나는 형태들을 말하며 압축, 포화, 과열 등의 상태를 말합니다.
[열역학] 5. Properties of Pure Substances 1 (순수 물질, 상변화 과정)
순수한 물질 (Pure Substance)는 화학적 구성이 전체적으로 고정돼있는 상태를 말하며 즉 단일로 구성된 물질을 의미합니다. 이 물질들은 열역학에서 주요하게 다루는 물질들로 이유에 대해서는 순
domybestinlife.tistory.com
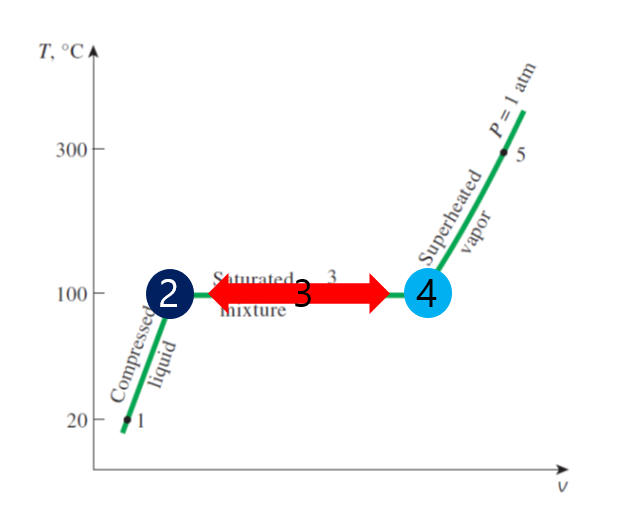
하단은 Property Table 입니다. 속성 테이블로써 각 온도와 압력에 따른 특정 순수 물질의 Property를 적어둔 것입니다. 그리고 해당 표를 보기 위해서 왼쪽 그림의 구간에 대해 다시 설명을 드리면 2번은 포화액, 3번 구간은 mixture, 4번 구간은 포화 증기 구간입니다.
 |
 |
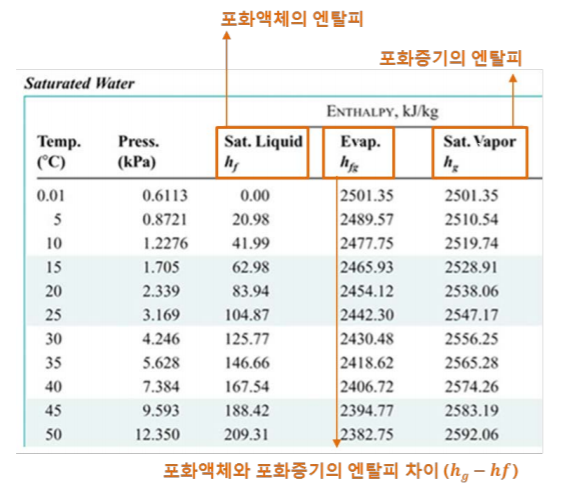
- \(v_f\) : 포화액의 비체적
- \(v_g\) : 포화증기의 비체적
- \(v_fg\) : \(v_g\) - \(v_f\) 즉 포화 증기의 비체적과 포화액의 비체적의 차이입니다.
* 마찬가지로 \(h_fg\)는 증기의 잠열로써 증기화가 되기 위해서 포화액의 단위 질량당 필요한 에너지를 말합니다.
언급된 해당 개념들은 하단의 table처럼 제시가 되어있습니다. 때문에 차이를 구하기 위해서 뺄셈을 하지 않으셔도 됩니다.
Saturated Liquid-Vapor Mixture
포화액과 증기의 혼합 구간에서 증기의 질량이 전체 질량 중 얼마나 차지하는가를 나타내는 수치가 있습니다.
해당 수치는 바로 Quality로써 \(x\) 라고 표시하며 건도라고 읽습니다. 건도는 전체 질량에 대해서 얼마나 증기가 차지하는가를 비율로 나타낸 수로써 0~1 사이의 숫자로 표현합니다.
즉 0일 때는 Saturated Liquid (포화액)이며 1일 때는 Saturated Vapor (포화증기)를 나타냅니다. 수식은 다음과 같습니다.
 |
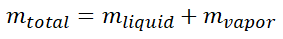 |
건도를 파악함으로써 포화 구간에서의 평균적인 비체적과 엔탈피, 그리고 내부에너지를 구할 수가 있습니다.

상단의 그림에서 우선 건도는 전체 포화구간포화 구간 길이 AC에 대한 AB의 비율입니다. 그리고 \(v_fg\)는 포화 구간에서 포화 증기와 포화액 비체적의 차이를 나타내는 것(시작과 끝)입니다. 이는 곧 AC를 의미합니다.
AB길이는 B 지점의 비체적을 \(v_avg\)라고 표현할때 포화액의 비체적과의 차이가 바로 AB 길이가 되겠습니다.

이를 이용하여 B 지점의 평균 비체적은 다음과 같이 나타냅니다.
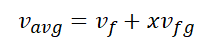
마찬가지로 건도를 활용하여 특정한 1차함수를 만들 수 있으며
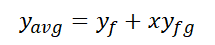
포화 구간에서의 평균 (비) 내부 에너지 및 (비) 엔탈피는 다음과 같습니다.

Superheated Vapor
포화구간을 넘어서 과열 증기 구간에서는 온도와 압력이 특성에 의존적이었던 포화 구간과는 달리 온도와 압력은 특성에 대해 독립적인 특성을 보이는 구간입니다.
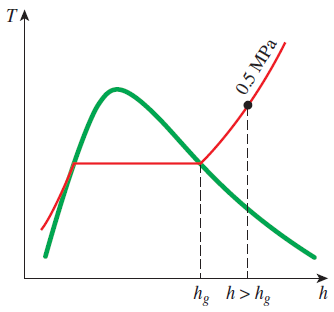
과열증기에서 보이는 특징은 다음과 같습니다.
- 특정 T에 대해서 포화압력 보다 낮은 압력
- 특정 P에 대해서 포화온도 보다 높은 온도
- 특정 P와 T에 대해서 포화증기 비체적 보다 높은 비체적
- 특정 P와 T에 대해서 포화증기 내부 에너지보다 높은 내부 에너지
- 특정 P와 T에 대해서 포화증기 엔탈피 보다 높은 엔탈피
Compressed Liquid
압축액 구간에서는 액체 구간이기 때문에 포화액 상태의 특성과 이하의 특성 값은 근사하다고 판단할 수 있습니다.
때문에 주어진 온도에 대해서 압축액구간의 특성은 특정 온도에서의 포화 값은 곧 압축액 구간의 값과 근사하다고 판별 가능하며 이는 곧 비 내부 에너지, 비체적, 비 엔탈피에도 적용이 가능합니다.

 |
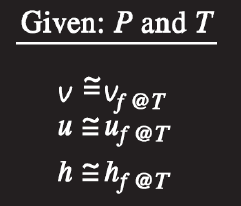 |
압축액에서 보이는 특징은 다음과 같습니다.
- 특정 T에 대해서 포화압력 보다 높은 압력
- 특정 P에 대해서 포화온도 보다 낮은 온도
- 특정 P와 T에 대해서 포화액 비체적 보다 낮은 비체적
- 특정 P와 T에 대해서 포화액 내부 에너지보다 낮은 내부 에너지
- 특정 P와 T에 대해서 포화액 엔탈피 보다 낮은 엔탈피
The Ideal-Gas Equation of State
상태 방정식은 압력과 온도 그리고 물질의 비체적과 관련된 방정식입니다. 해당 식은 매우 간단하며 가스 상태에서 매우 잘 알려진 식으로써 P-v-T에 대한 가스(증기)의 행동 특성을 예측할 때 활용되며 꽤나 특정한 구간에 대해서는 정확한 결과를 보여줍니다.
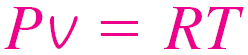

| R : 기체 상수 | M : 몰 질량 (kg/kmol) | \(R_u\) : 보편 기체 상수 ( Universal gas constant ) |
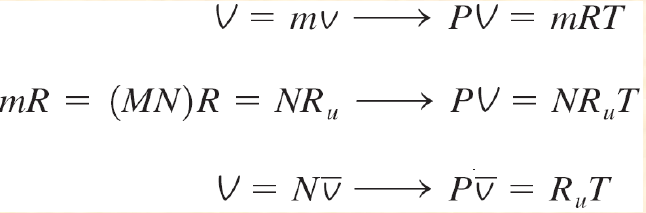
* 다양한 물질의 기체 상수 값
| 물질 (Substance) | R, KJ/kg.k |
| Air | 0.2870 |
| Helium | 2.0769 |
| Argon | 0.2081 |
| Nitrogen | 0.2968 |
읽어주셔서 감사합니다.
다음 글에서는 닫힌계, Closed System에서 열역학 제 1법칙을 활용한 계산에 대해서 적어보겠습니다.
'전공 관련 (Major) > 열 역학 (Thermodynamics)' 카테고리의 다른 글
| [열역학] 8. Mass & Energy Analysis of Control Volume 1.5 ( 일과 열의 출입에 따른 부호 ) (0) | 2021.01.03 |
|---|---|
| [열역학] 7. Mass & Energy Analysis of Control Volume 1 (질량 유량,유동일, 유동에너지, 정상상태 유동) (0) | 2021.01.03 |
| [열역학] 5. Properties of Pure Substances 1 (순수 물질, 상변화 과정) (0) | 2020.12.24 |
| [열역학] 4. Energy Transfer & General Energy Analysis (0) | 2020.12.24 |
| [열역학] 3. Heat, Work & 경로, 상태 함수 & 열역학 제 1법칙 (0) | 2020.12.24 |




댓글