Convolution
합성곱의 공학적인 사용 목적은 선형(Linear) 및 시간 불변 시스템 (Time-invariant System - LTI)에서 입력에 대한 출력을 보기 위해서 사용된다.
간단히 convolution의 의미에 대해 말하자면 시스템에 메모리가 있는 경우 한 시스템의 출력이 현재 입력에 의해서만 결정되는 것이 아닌 이전 입력(causal system이라면)에 의해서도 영향을 받기 때문에 그에 대한 출력을 나타내기 위해 하는 연산이다.
기호로는 * 을 의미하며 하나의 함수와 또 다른 함수를 반전(Reverse), 이동(Shift) 한 결과를 곱하여 구간에 대한 적분을 통한 새로운 함수를 구하는 연산자이다. 반전을 한 이유는 처음 발생한 신호가 당연히 f(t)와 먼저 만나야하기 때문에 y축 대칭을 해줘야 한다. 즉 입력을 반전시키지 않으면 처음에 약한 신호가 들어가고 나중에 강한 신호가 나와서 시간적으로 반대로 된 신호가 나오기 때문이다.
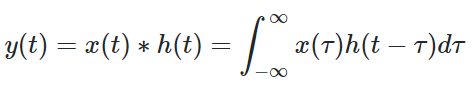
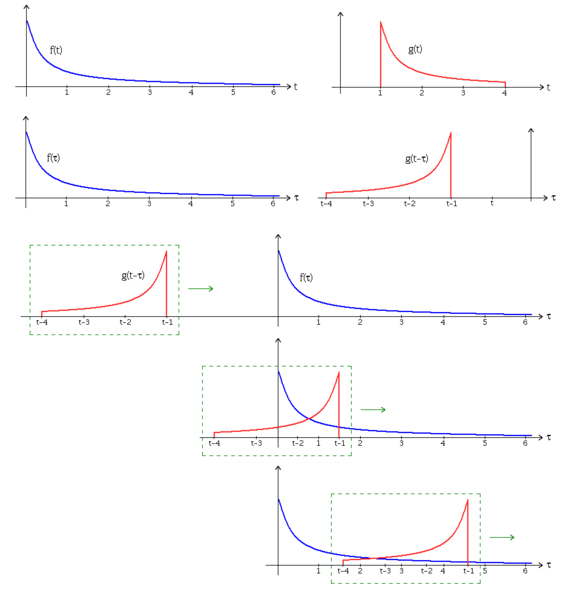
예를 들어서 북을 막대기로 칠때 나는 소리는 내부 공명과 칠 때의 소리가 어우러져서 발생하게 된다. 처음에 막대기로 북을 때릴 때는 순간적으로 임펄스 즉 순간적으로 부딪침에 의해서 나오는 소리가 나오지만 이후 따라 친다면 임펄스와 공명이 같이 소리를 만들게 된다. 즉 임펄스와 공명이 합쳐진 형태로 시스템이 만들어지게 된다.
임펄스 * 내부 공명 = 출력 (Response)
보통 시스템을 연속시간영역에서 상태 방정식을 수립하게 된다. 이때 해당 식을 라플라스 역변환을 통해서 상태천이 행렬(State Transition Matrix)을 구할 수 있으면, 컨볼루션 convolution을 활용하여 시간영역에서의 해를 구할 때 사용되기도 한다.
Convolution 연산의 성질
1. 교환 법칙 : f * g = g * f
2. 결합 법칙 : f * ( g * h ) = ( f * g ) * h
3. 분배 법칙 : f * ( g + h ) = ( f * g ) + ( f * h )
4. 스칼라 곱의 결합 법칙 : a(f * g) - (af) * g = f * (ag)
* Matlab 코드
clc; close all; clear all;
%%
fs = 200;
t = linspace(-1,1,fs);
crossCorrelation = zeros(1,length(t));
convolution = zeros(1,length(t));
set(gcf,'Color',[1 1 1]);
ax = [-1 1 -0.2 1.1];
disp('y1: single rectangle pulse with width of 1.0')
disp('y2: single triangle pulse with width of 0.5')
y1 = rectpuls(t,1);
y2 = tripuls(t,0.5,-1);
subplot(4,2,1); plot(t,y1,'Color','blue','LineWidth',2),axis(ax);
grid on;
xlabel('t'), ylabel('y1')
subplot(4,2,2); plot(t,y2,'Color','red','LineWidth',2),axis(ax);
grid on;
xlabel('t'), ylabel('y2')
disp('Press Enter to continue');
pause;
%%
iter = length(t);
%grid on;
for i = 1:iter
moveStep = (2*i-fs)/fs;
y2_shifted = tripuls(t-moveStep,0.5,-1);
crossCorrelation(i) = trapz(t, y1.*y2_shifted);
subplot(4,2,3:4)
plot(t,y1,'Color','blue','LineWidth',2),axis(ax); grid on;
hold on;
plot(t,y2_shifted,'Color','red', 'LineWidth',2),axis(ax);
xlabel('t')
hold off;
subplot(4,2,5:6)
plot(t(1:i),crossCorrelation(1:i),'Color','black','LineWidth',2); axis([-1 1 -0.2 0.5]); grid on;
xlabel('t'), ylabel('CrossCorrelation - (y1, y2)(t)');
pause(0.01);
end
disp('Press Enter to continue');
pause;
'전공 관련 (Major) > 배터리 & BMS' 카테고리의 다른 글
| 유기(Organic) vs 무기(Inorganic) 화합물 (0) | 2021.10.11 |
|---|---|
| 메탈 에어 배터리 (Metal-Air Battery) (2) | 2021.07.11 |
| [BMS] - Battery Management System ( 배터리 관리 시스템 ) (0) | 2020.12.31 |
| [BMS] SOC 추종 알고리즘 전류 적산법 (0) | 2020.12.23 |
| [BMS] SOC 직접 추종 방법1 ( OCV, 개방 회로 전압 ) (4) | 2020.12.23 |
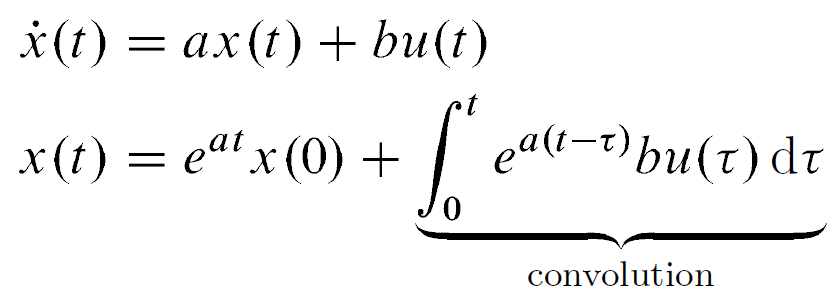




댓글