신경망은 아주 오래된 연구분야입니다.
오늘날 가장 광범위하게 쓰이고 있는 신경망의 정의입니다
' 신경망이란, 적응성이 있는 단순 단위로 구성된 광범위하고 서로 연결된 네트워크이다. 이 조직은 현실 세계 사물에 대한 생물 신경 계통의 상호작용을 모방할 수 있다. ' - Kohonen, 1988
머신러닝에서는 해당 개념에 학습을 더하여서 사용하는데 우선 신경망 학습에 대한 기초 성분이 있는데 바로 뉴런(Neuron) 입니다. 사람을 포함한 생물의 기초 단위로써 생물의 신경망에서 뉴런들끼리 서로 연결되어 있습니다. 만약 이러한 뉴런들이 신호를 받아 흥분을 하게 되었을 때 연결된 뉴런에게 화학물질을 전송하게끔 구성돼있습니다. 그러나 신호를 받아 흥분을 하게끔 하는 어떠한 한계치가 있는데 해당 한계치를 넘어야 자극이라고 느끼게 됩니다. 해당 한계치가 바로 임곗값(Threshold)입니다.
그리고 Threshold의 값을 넘음으로써 뉴런이 활성되며 다른 뉴런을 향해 화학물질을 전송하게 됩니다.
1943년, McCulloch and Pitts는 뉴런을 간단한 모델로 표현하는데 해당 모델이 M-P 뉴런 모델 입니다.
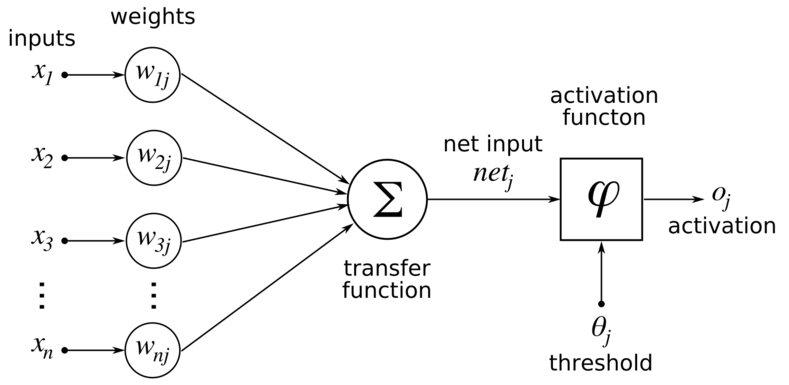
어떠한 d개의 입력이 들어오고 각각의 가중치가 매겨집니다. 그리고 뉴런이 받은 총 입력값은 임계값과 비교되고 활성화 함수(activation function, ex - sigmoid function)를 통해 출력이 나오게 됩니다.

활성화 함수의 역할은 입력 신호의 총합을 그대로 사용하지 않고, 출력 신호로 변환하는 함수로써 입력 신호의 총합이 활성화를 일으키는지 아닌지를 정하는 역할을 합니다.
퍼셉트론은 임계값을 경계로 출력이 바뀌는데 이는 활성화 함수로 '계단 함수'를 사용하는 신경망입니다.
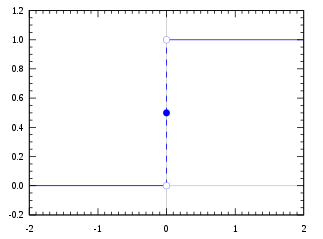
계단 함수의 특징은 출력 값을 0 또는 1로 투영시키는 역할로써 1은 뉴런의 '흥분'상태를 말하며 0은 뉴런의 '억제' 상태를 말합니다. 그러나 단위 계단 함수 같은 경우 불연속적인 특성을 지니기 때문에 다양한 출력을 표현하지 못합니다.
def h(result):
if result < 0:
return 0
else:
return 1때문에 신경망 쪽에서는 시그모이드 함수를 자주 사용하기도 하는데 0과 1 사이에서 움직이면서 0과 1사이 값을 골고루 받을 수 있는 장점을 가지기 때문에 가중치에 따라 연산된 값이 내가 찾으려는 값과 가까운지 아닌지를 판단할 수 있습니다. 보통 기준이 되는 포인트가 바로 0.5이며 0.5보다 크면 true에 가깝다고도 판단할 수 있게 됩니다. 비교적 넓은 범위 내에서 변화하는 입력값을 0과 1 사이로 출력할 수 있기에 스쿼싱 함수(Squasing function)이라고도 합니다.

def sigmoid(x):
return 1 / (1 + np.exp(-x))그 외에도 Tanh, ReLU(Rectified Linear Unit)나 LeakyReLu 같은 여러 활성화 함수가 존재합니다.
퍼셉트론 (Perceptron)
퍼셉트론은 두 개의 뉴런으로 구성되어 입력층이 외부 입력 신호를 받은 후 출력층으로 전달하는 구조입니다. 출력층은 M-P 뉴런이며 이를 임계값 논리 단위(Threshold logic unit)라고 부릅니다.
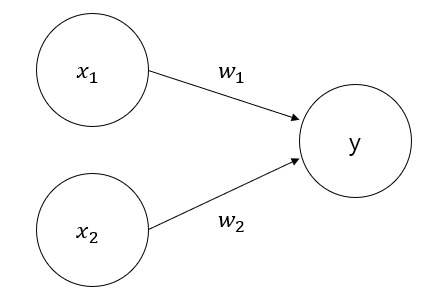
퍼셉트론은 쉽게 AND, OR, NAND 논리를 계산 가능합니다.

해당 식에서 만약 f가 단위 계단 함수일 때를 가정해봅니다.
- AND ( x1 ^ x2) : w1=w2=1, theta = 2이면 y=f(1x1 + 1x2 - 2)이고, x1=x2=1일 때만 y=1이다.
- OR (x1 v x2) : w1=w2=1, theta=0.5, 이면 y=f(1x1 + 1x2 - 0.5)이고, x1=1 혹은 x2=1일 때 y=1이다.
- NAND : w1=-0.6, w2=0, theta = -0.5일 때 y=f(-0.6x1 + 0x2 + 0.5)이고 x1=1일 때 y=0이고 x1=0일 때 y=1이다.
일반적으로 training data(학습 데이터)를 통해서 가중치 w와 임계값 theta를 얻게 됩니다. 퍼셉트론에서 학습 규칙은 다음과 같습니다. 훈련 샘플 x와 y가 존재할 때 출력이 y 헷이라면 퍼셉트론의 가중치는 다음과 같이 조정됩니다.

여기서 시그마는 0,1 사이의 값을 가지며 학습률(Learning Rate)이라는 역할을 합니다. 첫 번째 식을 통해서 만약 퍼셉트론이 훈련 샘플 x, y에 대해 정확히 예측 가능할 때 y헷과 y가 동일할 때 퍼셉트론에는 아무런 변화가 일어나지 않게 됩니다. 다만 틀릴 경우에는 해당 차이만큼 가중치가 변화하게 되는 구조로 구성됩니다. 주의해야 할 점은 퍼셉트론은 출력 측 뉴런만 활성화 함수 처리를 합니다. 즉 오직 한 층의 기능성 뉴런만 보유하기에 학습능력이 매우 제한적입니다.
사실 위에서 언급된 논리회로 문제는 모두 선형 분리가 가능한 문제인데 다음과 같이 선형 초평면으로 클래스를 분리 가능할 때 퍼셉트론의 학습 프로세스는 반드시 수렴되며 적절한 가중치 w를 찾게 됩니다. 반대일 때는 변동이 일어나기 때문에 w가 불안해져서 해를 구할 수가 없게 됩니다.
다만 선형 분리가 불가능한 문제들에 대해서는 다층의 기능성 뉴런들을 이용해야 하는데 하단의 그림의 이층 퍼셉트론이 그 예입니다. 출력층과 입력층 사이에 한층의 뉴런이 있는데 이를 은닉층 (Hidden Layer)라고 부릅니다. 그리고 은닉층과 출력층 뉴런은 바디 활성화 함수의 기능을 가집니다.

그리고 자주 사용되는 신경망은 하단과 같이 겹층 구조를 이루고 있습니다. 각 층의 뉴런은 다음 층 뉴런과 정말 연결되어 있으며 같은 층의 뉴런끼리는 연결되어 있지 않습니다. 그리고 층을 뛰어넘는 연결도 존재하지 않습니다.

이러한 신경망 연결 결합 구조를 다층 순방향 신경망 (Multi-Layer feedforward Neural Networks)라고 부릅니다. 입력층 뉴런은 외부 입력을 받아서 앞에 있는 은닉층 및 출력층을 통해서 신호가 가고 되며 최종 결과는 출력층 뉴런에 의해 나오게 됩니다. 중요한 것은 입력층 뉴런은 단지 입력만 받는 역할이며 중간과 끝인 은닉층과 출력층이 기능성 뉴런을 가지고 있는 것입니다. 왼쪽 그림은 단일 은닉층 신경망(Neural Networks with a Single Hidden Layer)라고 부릅니다. 그리고 우측 같은 경우는 이층 구조의 순방향 네트워크입니다.
이러한 구조를 지나면서 학습이 진행되며 훈련 데이터를 통해서 뉴런 간의 연결 가중치와 각 기능성 뉴런의 임계값만 조절하면 됩니다. 즉 신경망이 학습하는 것은 모두 연결 가중치와 임계값에 내재되어 있다는 뜻입니다.
'프로그래밍 ( Programming ) > 머신러닝 ( ML )' 카테고리의 다른 글
| [ML] Logistic Regression 설명 및 직접 구현해보기 (2) | 2021.12.02 |
|---|---|
| [ML] Cross validation(교차 검증)의 개념, 의미 (0) | 2021.11.22 |
| [ML] Linear Regression 선형 회귀 (0) | 2021.11.22 |
| [ML] 머신러닝 ( Machine Learning ) (0) | 2021.02.07 |
| 경사하강법 (Gradient descent) (0) | 2021.01.23 |




댓글